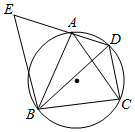
如图，四边形内接于圆，，对角线平分．

1. 如图，四边形 $\text{[math]}$ 内接于圆， $\text{[math]}$ ，对角线 $\text{[math]}$ 平分 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ 是等边三角形；

(2) 过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的面积．

【考点】

三角形全等及其性质; 三角形全等的判定; 等边三角形的判定与性质; 勾股定理; 圆的综合题; 几何图形的面积计算-割补法;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图①，有一组平行线l₁∥l₂∥l₃∥l₄ ，正方形ABCD的四个顶点分别在l₁、l₂、l₃、l₄上，EG过点D且垂直于l₁于点E，分别交l₂、l₄于点F、G，EF＝DG＝1，DF＝2.

(1) AE＝，正方形ABCD的边长＝；

(2) 如图②，将∠AED绕点A顺时针旋转α°得到∠AE′D′，且0°＜α＜90°，点D′在直线l₃上，以AD′为边在E′D′左侧作菱形AD′C′B′，使点B′、C′分别在直线l₂、l₄上．

①写出∠B′AD′与α的函数关系并给出证明；

②若α＝30°，求菱形AD′C′B′的边长．

综合题困难

2. 综合运用．

(1) 如图（ $\text{[math]}$ ），已知：在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为点 $\text{[math]}$ ， $\text{[math]}$ ．证明： $\text{[math]}$ ．

(2) 如图（ $\text{[math]}$ ），将（ $\text{[math]}$ ）中的条件改为：在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点都在直线 $\text{[math]}$ 上，并且有 $\text{[math]}$ ，其中 $\text{[math]}$ 为任意锐角或钝角．请问结论 $\text{[math]}$ 是否成立？如成立，请你给出证明；若不成立，请说明理由．

(3) 拓展与应用：如图（ $\text{[math]}$ ）， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点所在直线 $\text{[math]}$ 上的两动点（ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点互不重合），点 $\text{[math]}$ 为 $\text{[math]}$ 平分线上的一点，且 $\text{[math]}$ 和 $\text{[math]}$ 均为等边三角形，连接 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，试判断 $\text{[math]}$ 的形状并说明理由．

综合题普通

(1) 如图①，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 的顶点E，F分别在 $\text{[math]}$ ， $\text{[math]}$ 边上，高 $\text{[math]}$ 与正方形的边长相等，求 $\text{[math]}$ 的度数．

(2) 如图②，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点M，N是 $\text{[math]}$ 边上的任意两点，且 $\text{[math]}$ ，将 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 至 $\text{[math]}$ 位置，连接 $\text{[math]}$ ，试判断 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并说明理由．

(3) 在图①中，连接 $\text{[math]}$ 分别交 $\text{[math]}$ ， $\text{[math]}$ 于点M，N，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ， $\text{[math]}$ 的长．

综合题普通