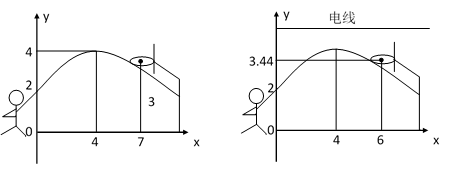
如图，在平面直角坐标系中，矩形的边与x轴、y轴的交点分别为，抛物线过B ， C两点，动点M从点D开始以每秒5个单位长度的速度沿的方向运动到达C点后停止运动．动点N从点O以每秒4个单位长度的速度沿方向运动，到达C点后，立即返回，向方向运动，到达O点后，又立即返回，依此在线段上反复运动，当点M停止运动时，点N也停止运动，设运动时间为．

0 返回首页

1. 如图，在平面直角坐标系中，矩形 $\text{[math]}$ 的边 $\text{[math]}$ 与x轴、y轴的交点分别为 $\text{[math]}$ ，抛物线 $\text{[math]}$ 过B ， C两点，动点M从点D开始以每秒5个单位长度的速度沿 $\text{[math]}$ 的方向运动到达C点后停止运动．动点N从点O以每秒4个单位长度的速度沿 $\text{[math]}$ 方向运动，到达C点后，立即返回，向 $\text{[math]}$ 方向运动，到达O点后，又立即返回，依此在线段 $\text{[math]}$ 上反复运动，当点M停止运动时，点N也停止运动，设运动时间为 $\text{[math]}$ ．

(1) 求抛物线的解析式；

(2) 求点D的坐标；

(3) 当点M ， N同时开始运动时，若以点M ， D ， C为顶点的三角形与以点B ， O ， N为顶点的三角形相似，求t的值；

(4) 过点D与x轴平行的直线，交抛物线的对称轴于点Q ，将线段 $\text{[math]}$ 沿过点B的直线翻折，点A的对称点为 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值．

【考点】

待定系数法求二次函数解析式; 两点之间线段最短; 轴对称的应用-最短距离问题; 相似三角形的判定与性质; 二次函数-动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 根据以下素材，探索完成任务．

如何调整蔬菜大棚的结构？
素材1	我国的大棚（如图1）种植技术已十分成熟，一块土地上有一个蔬菜大棚，其横截面顶部为抛物线型，大棚的一端固定在墙体 $\text{[math]}$ 上，另一端固定在墙体 $\text{[math]}$ 上，其横截面有2根支架 $\text{[math]}$ ，相关数据如图2所示，其中 $\text{[math]}$ ， $\text{[math]}$ ．
素材2	已知大棚有200根长为 $\text{[math]}$ 的支架和200根长为 $\text{[math]}$ 的支架，为增加棚内空间，拟将图2中棚顶向上调整，支架总数不变，对应支架的长度变化如图3所示，调整后C与E上升相同的高度，增加的支架单价为60元/米（接口忽略不计），现有改造经费32000元．
问题解决
任务1	确定大棚形状	在图2中以点O为原点， $\text{[math]}$ 所在直线为y轴建立平面直角坐标系，求抛物线的函数表达式．
任务2	尝试改造方案	当 $\text{[math]}$ 米，只考虑经费情况下，请通过计算说明能否完成改造．
任务3	拟定最优方案	只考虑经费情况下，求出 $\text{[math]}$ 的最大值．