如图四面体ABCD中，△ABC是正三角形，AD=CD．

1.

如图四面体ABCD中，△ABC是正三角形，AD=CD．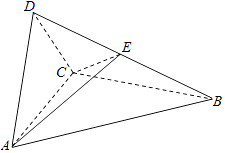

(1) 证明：AC⊥BD；

(2) 已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．

【考点】

棱柱、棱锥、棱台的体积; 直线与平面垂直的性质; 空间向量的数乘运算; 空间向量的数量积运算; 空间向量的线性运算的坐标表示;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图所示，在边长为2的菱形 $\text{[math]}$ 中， $\text{[math]}$ ，现将 $\text{[math]}$ 沿 $\text{[math]}$ 边折到 $\text{[math]}$ 的位置．

(1) 求证： $\text{[math]}$ ；

(2) 求三棱锥 $\text{[math]}$ 体积的最大值．

解答题普通

2. 如图，四棱柱 $\text{[math]}$ 的底面 $\text{[math]}$ 为菱形，且 $\text{[math]}$ .

(1) 证明：四边形 $\text{[math]}$ 为矩形；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ 平面 $\text{[math]}$ ，求四棱柱 $\text{[math]}$ 的体积.

解答题普通

3. 如图1，在边长为4的正三角形ABC中，D，F分别为AB，AC的中点，E为AD的中点．将△BCD与△AEF分别沿CD，EF同侧折起，使得二面角A﹣EF﹣D与二面角B﹣CD﹣E的大小都等于90°，得到如图2所示的多面体．

(1) 在多面体中，求证：A，B，D，E四点共同面；

(2) 求多面体的体积．

解答题普通