0 返回首页
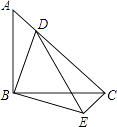
1. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D是BC边上一动点，连接AD，把AD绕点A逆时针旋转90°，得到AE，连接CE，DE.点F是DE的中点，连接CF.

(1) 求证：CF＝ AD；
(2) 如图2所示，在点D运动的过程中，当BD＝2CD时，分别延长CF，BA，相交于点G，猜想AG与BC存在的数量关系，并证明你猜想的结论；
(3) 在点D运动的过程中，在线段AD上存在一点P，使PA+PB+PC的值最小.当PA+PB+PC的值取得最小值时，AP的长为m，请直接用含m的式子表示CE的长.
【考点】
等边三角形的判定与性质; 勾股定理; 旋转的性质; 等腰直角三角形; 三角形全等的判定-SAS;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 已知点P为线段AB上一点，将线段AP绕点A逆时针旋转 ， 得到线段AC；再将线段BP绕点B逆时针旋转 ， 得到线段BD；连接CP，DP，AD，取AD中点M，连接BM，BC．

(1) 当时，

①如图1，若点P为AB中点，直接写出∠CBM的度数为，线段BC与BM的数量关系为．

②如图2，若点P不为AB中点时，请探究线段BC与BM的数量关系，并说明理由．
(2) 如图3，若PA＝PB＝2，当∠CPB＝105°时，请直接写出的值．
综合题 困难
2. 如图，等腰Rt△ABC中，BA=BC，∠ABC=90°，点D在AC上，将△ABD绕点B沿顺时针方向旋转90°后，得到△CBE．

(1) 求∠DCE的度数；
(2) 若AB=4，CD=3AD，求DE的长．
综合题 普通
3. 如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，Q为AB的中点．动点P从点A出发沿折线AC--CB以每秒2个单位长度的速度运动，连结PQ，以PQ为边构造正方形PMNQ且边MN与点B始终在边PQ同侧．设点P的运动时间为t秒(>0)．

(1) 线段AB的长为
(2) 当点P在边AC上运动时，线段CP的长为      ▲ (用含t的代数式表示) ．

①当正方形PMNQ与△ABC重叠部分图形是正方形时，求t的取值范围．

②当边MN的中点落在△ABC的边上时，求正方形PMNQ的面积．
(3) 当点P不与点C重合时，作点C关于直线PQ的对称点C'当PC'⊥AB时，直接写出t的值．
综合题 普通