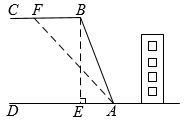
实验学校某班开展数学“综合与实践”测量活动．有两座垂直于水平地面且高度不一的圆柱，两座圆柱后面有一斜坡，且圆柱底部到坡脚水平线的距离皆为．王诗嬑观测到高度矮圆柱的影子落在地面上，其长为；而高圆柱的部分影子落在坡上，如图所示．已知落在地面上的影子皆与坡脚水平线互相垂直，并视太阳光为平行光，测得斜坡坡度，在不计圆柱厚度与影子宽度的情况下，请解答下列问题：

1. 实验学校某班开展数学“综合与实践”测量活动．有两座垂直于水平地面且高度不一的圆柱，两座圆柱后面有一斜坡，且圆柱底部到坡脚水平线 $\text{[math]}$ 的距离皆为 $\text{[math]}$ ．王诗嬑观测到高度 $\text{[math]}$ 矮圆柱的影子落在地面上，其长为 $\text{[math]}$ ；而高圆柱的部分影子落在坡上，如图所示．已知落在地面上的影子皆与坡脚水平线 $\text{[math]}$ 互相垂直，并视太阳光为平行光，测得斜坡坡度 $\text{[math]}$ ，在不计圆柱厚度与影子宽度的情况下，请解答下列问题：

(1) 若王诗嬑的身高为 $\text{[math]}$ ，且此刻她的影子完全落在地面上，则影子长为多少 $\text{[math]}$ ？

(2) 猜想：此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内．请直接回答这个猜想是否符合题意？

(3) 若同一时间量得高圆柱落在坡面上的影子长为 $\text{[math]}$ ，则高圆柱的高度为多少 $\text{[math]}$ ？

【考点】

相似三角形的性质; 解直角三角形的实际应用﹣坡度坡角问题; 平行投影;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，山区某教学楼后面紧邻着一个土坡，坡面BC平行于地面AD，斜坡AB的坡比为i=1： $\text{[math]}$ ，且AB=26米．

(1) 求坡顶与地面的距离BE的长．

(2) 为了防止山体滑坡，保障安全，学校决定对该土坡进行改造．经地质人员勘测，当坡角不超过53°时，可确保山体不滑坡．学校计划将斜坡AB改造成AF(如图所示)，那么BF至少是多少米？(结果精确到1米)(参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.33)．

综合题普通

2. 暑假期间，小明与小亮相约到某旅游风景区登山，需要登顶 $\text{[math]}$ 高的山峰，由山底A处先步行 $\text{[math]}$ 到达 $\text{[math]}$ 处，再由 $\text{[math]}$ 处乘坐登山缆车到达山顶 $\text{[math]}$ 处．已知点A，B．D，E，F在同一平面内，山坡 $\text{[math]}$ 的坡角为 $\text{[math]}$ ，缆车行驶路线 $\text{[math]}$ 与水平面的夹角为 $\text{[math]}$ （换乘登山缆车的时间忽略不计）

(1) 求登山缆车上升的高度 $\text{[math]}$ ；

(2) 若步行速度为 $\text{[math]}$ ，登山缆车的速度为 $\text{[math]}$ ，求从山底A处到达山顶 $\text{[math]}$ 处大约需要多少分钟（结果精确到 $\text{[math]}$ ）

（参考数据： $\text{[math]}$ ）

综合题普通

3. 贵州旅游资源丰富．某景区为给游客提供更好的游览体验，拟在如图①景区内修建观光索道．设计示意图如图②所示，以山脚 $\text{[math]}$ 为起点，沿途修建 $\text{[math]}$ 、 $\text{[math]}$ 两段长度相等的观光索道，最终到达山顶 $\text{[math]}$ 处，中途设计了一段与 $\text{[math]}$ 平行的观光平台 $\text{[math]}$ 为 $\text{[math]}$ ．索道 $\text{[math]}$ 与 $\text{[math]}$ 的夹角为 $\text{[math]}$ ， $\text{[math]}$ 与水平线夹角为 $\text{[math]}$ ， $\text{[math]}$ 两处的水平距离 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ．（图中所有点都在同一平面内，点 $\text{[math]}$ 在同一水平线上）

(1) 求索道 $\text{[math]}$ 的长（结果精确到 $\text{[math]}$ ）；

(2) 求水平距离 $\text{[math]}$ 的长（结果精确到 $\text{[math]}$ ）．

（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

综合题普通