1.
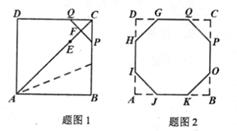
小明对教材“课题学习”中的“用一张正方形折出一个正八边形”的问题进行了认真的探索。他先把正方形ABCD沿对角线AC对折,再把∠BAC对折,使点B落在AC上,记为点E,然后沿CE的中垂线折叠,得到折痕PQ,如图1,类似地,折出其余三条折痕GH,IJ,KO,得到八边形GHIJKOPQ,如图2。
(1)
求证:△CPQ是等腰直角三角形。
(2)
若AB=a,求PQ的长。(用含a的代数式表示)
(3)
我们把八条边长相等,八个内角都相等的八边形叫做正八边形.试说明八边形GHIJKOPQ是正八边形,请把过程补充完整。
解:理由如下:
① 
∴∠GQP=135°
同理可得:∠QPO=∠POK=∠OKJ=∠KJI=∠JIH=∠IHG=∠HGQ=135°。
② 
∴PQ=QG。
同理可得:QG=GH=HI=IJ=JK=KO=PO=PQ
∴八边形GHIJKOPQ是正八边形。
【考点】
正方形的性质;
圆内接正多边形;
翻折变换(折叠问题);
等腰直角三角形;
能力提升