已知：如图，圆O是△ABC的外接圆，AO平分∠BAC ．

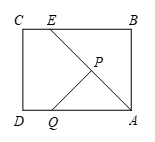
1. 已知：如图，圆O是△ABC的外接圆，AO平分∠BAC ．

(1) 求证：△ABC是等腰三角形；

(2) 当OA＝4，AB＝6，求边BC的长．

【考点】

全等三角形的判定与性质; 等腰三角形的判定与性质; 勾股定理; 垂径定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为边 $\text{[math]}$ 上一点， $\text{[math]}$ ，连接 $\text{[math]}$ ．动点 $\text{[math]}$ 从点 $\text{[math]}$ 同时出发，点 $\text{[math]}$ 以 $\text{[math]}$ 的速度沿 $\text{[math]}$ 向终点 $\text{[math]}$ 运动；点 $\text{[math]}$ 以 $\text{[math]}$ 的速度沿折线 $\text{[math]}$ 向终点 $\text{[math]}$ 运动．设点 $\text{[math]}$ 运动的时间为 $\text{[math]}$ ，在运动过程中，点 $\text{[math]}$ ，点 $\text{[math]}$ 经过的路线与线段 $\text{[math]}$ 围成的图形面积为 $\text{[math]}$ ．

(1) $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ °；

(2) 求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式，并写出自变量 $\text{[math]}$ 的取值范围；

(3) 当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的值．

综合题普通

2. 如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，Q为AB的中点．动点P从点A出发沿折线AC--CB以每秒2个单位长度的速度运动，连结PQ，以PQ为边构造正方形PMNQ且边MN与点B始终在边PQ同侧．设点P的运动时间为t秒(>0)．

(1) 线段AB的长为

(2) 当点P在边AC上运动时，线段CP的长为 ▲ (用含t的代数式表示) ．

①当正方形PMNQ与△ABC重叠部分图形是正方形时，求t的取值范围．

②当边MN的中点落在△ABC的边上时，求正方形PMNQ的面积．

(3) 当点P不与点C重合时，作点C关于直线PQ的对称点C'当PC'⊥AB时，直接写出t的值．

综合题普通

3. 如图，在四边形ABCD中，AB∥CD，∠ECF＝∠BCD＝90°，CE＝CF＝5，BC＝7，BD平分∠ABC，E是△BCD内一点，F是四边形ABCD外一点.（E可以在△BCD的边上）

(1) 求证：DC＝BC；

(2) 当∠BEC＝135°，设BE＝a，DE＝b，求a与b满足的关系式；

(3) 当E落在线段BD上时，求DE的长.

综合题普通