如图，正方形ABCD的边长为6，E、F分别是边CD、AD上动点，AE和BF交于点G.

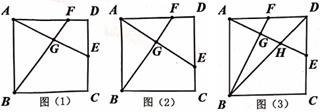
1. 如图，正方形ABCD的边长为6，E、F分别是边CD、AD上动点，AE和BF交于点G.

(1) 如图（1），若E为边CD的中点，AF=2FD，求AG的长.

(2) 如图（2），若点F在AD上从A向D运动，点E在DC上从D向C运动，两点同时出发，同时到达各自终点，求在运动过程中，点G运动的路径长。

(3) 如图（3），若E、F分别是边CD、AD上的中点，BD与AE交于点H，求∠FBD的正切值。

【考点】

全等三角形的判定与性质; 勾股定理; 正方形的性质; 锐角三角函数的定义; 等腰直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，四边形ABCD、BEFG均为正方形，连接AG、CE．

(1) 求证：AG=CE；

(2) 求证：AG⊥CE．

综合题普通

2. 勾股定理是数学史上非常重要的一个定理．早在2000多年以前，人们就开始对它进行研究，至今已有几百种证明方法．在欧几里得编的《原本》中证明勾股定理的方法如下，请同学们仔细阅读并解答相关问题：如图；分别以Rt△ABC的三边为边长，向外作正方形ABDE、BCFG、ACHI．

(1) 设正方形ABDE的面积为 $\text{[math]}$ ，正方形BCFG的面积为 $\text{[math]}$ ，正方形ACHI的面积为 $\text{[math]}$ ，证明 $\text{[math]}$ ；

(2) 连接BI、CE，求证：EC＝BI；

(3) 过点B作AC的垂线，交AC于点M，交IH于点N．试说明四边形AMNI与正方形ABDE的面积相等．

综合题普通

3. 如图，正方形ABCD和正方形AEFG有公共点A，点B在线段DG上.

(1) 判断DG与BE的位置关系，并说明理由：

(2) 若正方形ABCD的边长为2，正方形AEFG的边长为2 $\text{[math]}$ ，求BE的长.

综合题普通