1.
（概念认识）
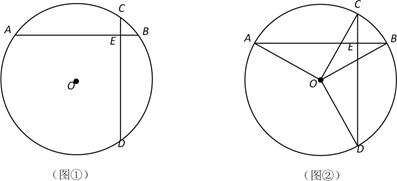
在同一个圆中两条互相垂直且相等的弦定义为“等垂弦”，两条弦所在直线的交点为等垂弦的分割点.如图①，AB、CD是⊙O的弦，AB＝CD，AB⊥CD，垂足为E，则AB、CD是等垂弦，E为等垂弦AB、CD的分割点.
(1)
（数学理解）
(2)
在⊙O中，⊙O的半径为5，E为等垂弦AB、CD的分割点， 
.求AB的长度.
(3)
（问题解决）
如图②，AB是⊙O的弦，作OC⊥OA、OD⊥OB，分别交⊙O于点C、D，连接CD.求证： AB、CD是⊙O的等垂弦.
AB、CD是⊙O的两条弦，CD＝ AB，且CD⊥AB，垂足为F.
①在图③中，利用直尺和圆规作弦CD（保留作图痕迹，不写作法）.
②若⊙O的半径为r，AB＝mr（m为常数），垂足F与⊙O的位置关系随m的值变化而变化，直接写出点F与⊙O的位置关系及对应的m的取值范围.
【考点】
全等三角形的判定与性质;
勾股定理;
正方形的判定与性质;
圆心角、弧、弦的关系;
圆周角定理;
能力提升
