1.
综合与实践
(问题情境)
在综合与实践课上,同学们以“矩形的折叠”为主题展开数学活动,如图1,在矩形纸片ABCD中,AB=4,BC=5,点E,F分别为边AB,AD上的点,且DF=3。
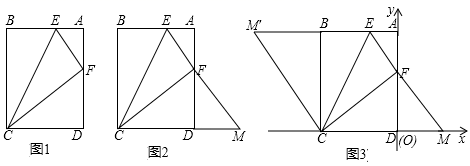
(操作发现)
(1)
沿CE折叠纸片,B点恰好与F点重合,求AE的长;
(2)
如图2,延长EF交CD的延长线于点M,请判断△CEM的形状,并说明理由。
(3)
(深入思考)
把图2置于平面直角坐标系中,如图3,使D点与原点O重合,C点在x轴的负半轴上,将△CEM沿CE翻折,使点M落在点M′处.连接CM′,求点M′的坐标.
【考点】
坐标与图形性质;
等腰三角形的判定;
勾股定理;
矩形的性质;
翻折变换(折叠问题);
能力提升


