1.
如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),

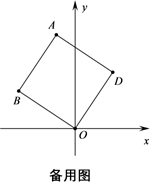
(1)
点B的坐标为;
(2)
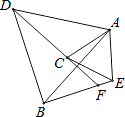
若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是▲ , 并说明理由;
(3)
在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在 P点运动过程中当EF取最小值时,此时∠DFE=°;
(4)
在(1)的条件下,点 M在 x 轴上,在平面内是否存在点N,使以 B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
【考点】
全等三角形的判定与性质;
等边三角形的性质;
菱形的性质;
正方形的性质;
等腰直角三角形;