0 返回首页
1.

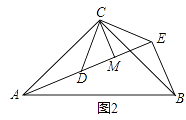
已知，如图，Rt△ABC中，∠ACB=90°，BC=8，cot∠BAC= ，点D在边BC上（不与点B、C重合），点E在边BC的延长线上，∠DAE=∠BAC，点F在线段AE上，∠ACF=∠B．设BD=x．

(1) 若点F恰好是AE的中点，求线段BD的长；
(2) 若y= ，求y关于x的函数关系式，并写出它的定义域；
(3) 当△ADE是以AD为腰的等腰三角形时，求线段BD的长．
【考点】
三角形的外角性质; 三角形全等及其性质; 三角形相关概念;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
换一批
1. 在现实生活中，我们会看到许多“标准”的矩形，如我们的课本封面、A4的打印纸等，其实这些矩形的长与宽之比都为 ：1，我们不妨就把这样的矩形称为“标准矩形”，在“标准矩形”ABCD中，P为DC边上一定点，且CP=BC，如图所示．

(1)

如图①，求证：BA=BP；
(2)

如图②，点Q在DC上，且DQ=CP，若G为BC边上一动点，当△AGQ的周长最小时，求 的值；
(3)

如图③，已知AD=1，在（2）的条件下，连接AG并延长交DC的延长线于点F，连接BF，T为BF的中点，M、N分别为线段PF与AB上的动点，且始终保持PM=BN，请证明：△MNT的面积S为定值，并求出这个定值．
综合题 普通
2.

已知：如图，在矩形ABCD中，AB=6cm，BC=8cm，对角线AC，BD交于点O，点P从点A出发，沿AD方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F．设运动时间为t（s）（0＜t＜6），解答下列问题：

(1) 当t为何值时，AP=PO．
(2) 设五边形OECQF的面积为S（cm2），试确定S与t的函数关系式；
(3) 在运动过程中，是否存在某一时刻t，使OD平分∠COP？若存在，求出t的值；若不存在，请说明理由．
综合题 普通
3.

问题探究：

如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．

(1) 证明：AD=BE；
(2) 求∠AEB的度数．
(3)

如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．（Ⅰ）请求出∠AEB的度数；（Ⅱ）判断线段CM、AE、BE之间的数量关系，并说明理由．
综合题 困难