1.
已知集合M是满足下列性制的函数f（x）的全体，存在实数a、k（k≠0），对于定义域内的任意x均有f（a+x）=kf（a﹣x）成立，称数对（a，k）为函数f（x）的“伴随数对”．
(1)
判断f（x）=x2是否属于集合M，并说明理由；
(2)
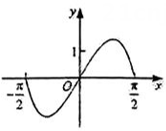
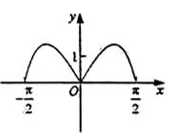
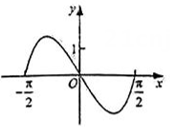
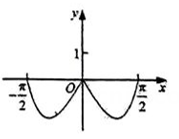
若函数f（x）=sinx∈M，求满足条件的函数f（x）的所有“伴随数对”；
(3)
若（1，1），（2，﹣1）都是函数f（x）的“伴随数对”，当1≤x＜2时，f（x）=cos（ 
x）；当x=2时，f（x）=0，求当2014≤x≤2016时，函数y=f（x）的解析式和零点．
【考点】
函数的值;
能力提升
真题演练
