1.
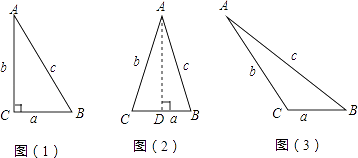
在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图1,则有a2+b2=c2;若△ABC为锐角三角形时,小明猜想:a2+b2>c2 , 理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,AD2=b2﹣x2 , 在Rt△ADB中,AD2=c2﹣(a﹣x)2
∴a2+b2=c2+2ax
∵a>0,x>0
∴2ax>0
∴a2+b2>c2
∴当△ABC为锐角三角形时,a2+b2>c2
所以小明的猜想是正确的.
(1)
请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系.
(2)
温馨提示:在图3中,作BC边上的高.
(3)
证明你猜想的结论是否正确.
【考点】
三角形三边关系;