0 返回首页
1.

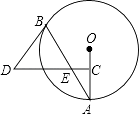
如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连AD．


(1) 求证：AD=AN
(2) 若AB=4 ， ON=1，求⊙O的半径
【考点】
垂径定理;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 一次函数 的图象与轴的负半轴相交于点 ，与 轴的正半轴相交于点 ，且 ． 的外接圆的圆心 的横坐标为 ．

(1) 求一次函数的解析式；
(2) 求图中阴影部分的面积．
综合题 普通
2. 如图1是一个用铁丝围成的篮框，我们来仿制一个类似的柱体形篮框．如图2，它是由一个半径为r、圆心角90°的扇形A2OB2 ， 矩形A2C2EO、B2D2EO，及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn ， OEFG围成，其中A1、G、B1在 上，A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上，C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上，EF⊥C2D2于H2 ， C1D1⊥EF于H1 ， FH1=H1H2=d，C1D1、C2D2、C3D3、CnDn依次等距离平行排放（最后一个矩形状框的边CnDn与点E间的距离应不超过d），A1C1∥A2C2∥A3C3∥…∥AnCn

(1) 求d的值；
(2) 问：CnDn与点E间的距离能否等于d？如果能，求出这样的n的值，如果不能，那么它们之间的距离是多少？
综合题 普通