0 返回首页
1. 对于平面直角坐标系xOy中的任意两点M（x1 ， y1），N（x2 ， y2），给出如下定义：点M与点N的“折线距离”为：d（M，N）＝|x1﹣x2|+|y1﹣y2|．

例如：若点M（﹣1，1），点N （2，﹣2），则点M与点N的“折线距离”为：d（M，N）＝|﹣1﹣2|+|1﹣（﹣2）|＝3+3＝6．

根据以上定义，解决下列问题：

(1) 已知点P （3，﹣2）．

①若点A（﹣2，﹣1），则d（P，A）＝；

②若点B（b，2），且d（P，B）＝5，则b＝；
(2) 已知点C（m，n）是直线y＝﹣x上的一个动点，且d（P，C）＜3，求m的取值范围．
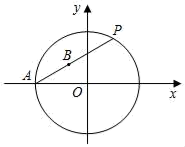
(3) ⊙F的半径为1，圆心F的坐标为（0，t），若⊙F上存在点E，使d（E，O）＝2，直接写出t的取值范围．
【考点】
坐标与图形性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1. 问题情境：

在平面直角坐标系xOy中有不重合的两点A（x1 ， y1）和点B（x2 ， y2），小明在学习中发现，若x1＝x2 ， 则AB∥y轴，且线段AB的长度为|y1﹣y2|；若y1＝y2 ， 则AB∥x轴，且线段AB的长度为|x1﹣x2|；

(1) （应用）：

①若点A（﹣1，1）、B（2，1），则AB∥x轴，AB的长度为.

②若点C（1，0），且CD∥y轴，且CD＝2，则点D的坐标为.
(2) （拓展）：

我们规定：平面直角坐标系中任意不重合的两点M（x1 ， y1），N（x2 ， y2）之间的折线距离为d（M，N）＝|x1﹣x2|+|y1﹣y2|；例如：图1中，点M（﹣1，1）与点N（1，﹣2）之间的折线距离为d（M，N）＝|﹣1﹣1|+|1﹣（﹣2）|＝2+3＝5.

解决下列问题：

①如图1，已知E（2，0），若F（﹣1，﹣2），则d（E，F）；

②如图2，已知E（2，0），H（1，t），若d（E，H）＝3，则t＝.

③如图3，已知P（3，3），点Q在x轴上，且三角形OPQ的面积为3，则d（P，Q）＝.
综合题 普通
2. 在平面直角坐标系xOy中，对于P、Q两点给出如下定义：若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值，则称P、Q两点为“等距点”，如图中的P、Q两点即为“等距点”．

(1) 已知点A的坐标为（﹣3，1）

①在点E（0，3）、F（3，﹣3）、G（2，﹣5）中，点A的“等距点”是；

②若点B在直线y＝x+6上，且A、B两点为“等距点”，则点B的坐标为；
(2) 直线l：y＝kx﹣3（k＞0）与x轴交于点C，与y轴交于点D．

①若T1（﹣1，t1）、T2（4，t2）是直线l上的两点，且T1、T2为“等距点”，求k的值；

②当k＝1时，半径为r的⊙O上存在一点M，线段CD上存在一点N，使得M、N两点为“等距点”，直接写出r的取值范围．
综合题 困难
3. 如图，在平面直角坐标系中，给出如下定义：已知点A（2，3），点B（6，3），连接AB．如果线段AB上有一个点与点P的距离不大于1，那么称点P是线段AB的“环绕点”．


(1) 已知点C（3，1.5），D（4，3.5），E（1，3），则是线段AB的“环绕点”的点是；
(2) 已知点P（m，n）在反比例函数y= 的图象上，且点P是线段AB的“环绕点”，求出点P的横坐标m的取值范围；
(3) 已知⊙M上有一点P是线段AB的“环绕点”，且点M（4，1），求⊙M的半径r的取值范围．
综合题 普通