1.
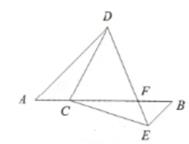
已知：在 
中， 
， 
，过点 
、 
分别作 
的垂线与过点 
的直线交于 
、 
两点.
(1)
如图1，求证： 
；
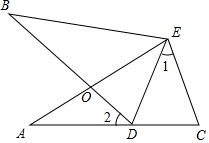
(2)
如图2，连接 
、 
相交于点 
，在不添加任何辅助线的情况下，请写出图2中的四对三角形，使写出的每对三角形面积相等.
【考点】
三角形的角平分线、中线和高;
全等三角形的判定与性质;
