1.
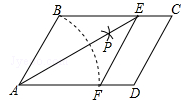
如图，在菱形ABCD中，边长为2 
，∠BAD＝120°，点P从点B开始，沿着B→D方向，速度为每秒1个单位，运动到点D停止，设运动的时间为t（秒），将线段AP绕点A逆时针旋转60°，得到对应线段的延长线与过点P且垂直AP的垂线段相交于点E，
（ ≈1.73，sin11°≈0.19，cos11°≈0.98，sin19°≈0.33，tan19°≈0.34，sin41°≈0.65，tan41°≈0.87）
(1)
当t＝0时，求AE的值.
(2)
P点在运动过程中，线段PE与菱形的边框交于点F.（精确到0.1）
(3)
当点P在运动过程中，求出△ACE的面积y关于时间t的函数表达式.（请说明理由）
问题1：如图2，当∠BAP＝11°，AF＝2PF，则OQ＝.
问题2：当t为何值时，△APF是含有30°角的直角三角形，写出所有符合条件的t的值.
【考点】
等边三角形的判定与性质;
含30°角的直角三角形;
菱形的性质;
相似三角形的判定与性质;
旋转的性质;
