定义：有一个内角为90°，且对角线相等的四边形称为准矩形. 图1 图2 图3

1. 定义：有一个内角为90°，且对角线相等的四边形称为准矩形.

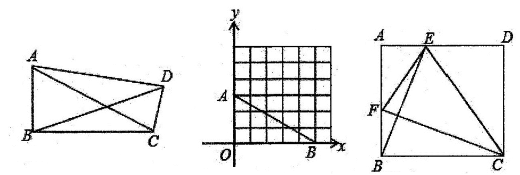
图1 图2 图3

(1) ①如图1，准矩形ABCD中，∠ABC=90°，若AB=2，BC=3，则BD=；

(2) 如图3，正方形ABCD中，点E、F分别是边AD、AB上的点，且CFLBE，求证：四边形BCEF是准矩形；

(3) 已知准矩形ABCD中，∠ABC=90°，∠BAC=60°，AB=2，当△ADC为等腰三角形时，请直接写出这个准矩形的面积是.

【考点】

矩形的性质; 正方形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知正方形ABCD的边长为1，正方形CEFG的面积为 $\text{[math]}$ ，点E在CD边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为 $\text{[math]}$ ，且 $\text{[math]}$ .

(1) 求线段CE的长；

(2) 若点H为BC边的中点，连结HD，求证： $\text{[math]}$ .

综合题困难

2. 如图，正方形ABCD的边长为1，点E是边AB上一点，过点，E作EF//BC．

(1) 设以线段AE，AD为邻边的矩形的面积为 $\text{[math]}$ ，以BE为边的正方形的面积为 $\text{[math]}$ ，且 $\text{[math]}$ ，求BE的长；

(2) 连结AC，DE，若H是DE的中点， $\text{[math]}$ 交AC于点G，连结EG，求证： $\text{[math]}$ ．

综合题普通

3. 如图，矩形ABCD ，过点B作BE∥AC交DC的延长线于点E ．过点D作DH⊥BE于H ， G为AC中点，连接GH ．

(1) 求证：BE＝AC ．

(2) 判断GH与BE的数量关系并证明．

综合题普通