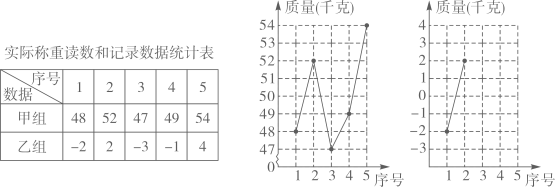
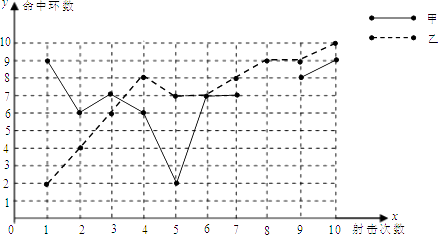
某厂生产A，B两种产品，其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了如表统计表及不完整的折线图．A，B产品单价变化统计表第一次第二次第三次 A产品单价（元/件） 6 5.2 6.5 B产品单价（元/件） 3.5 4 3并求得了A产品三次单价的平均数和方差：=5.9，sA2=[（6﹣5.9）2+（5.2﹣5.9）2+（6.5﹣5.9）2]=.

某厂生产A，B两种产品，其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了如表统计表及不完整的折线图．

A，B产品单价变化统计表

并求得了A产品三次单价的平均数和方差：

=5.9，s_A²= $\text{[math]}$ [（6﹣5.9）²+（5.2﹣5.9）²+（6.5﹣5.9）²]= $\text{[math]}$ .

(1) 补全如图中B产品单价变化的折线图．B产品第三次的单价比上一次的单价降低了 %.

(2) 求B产品三次单价的方差，并比较哪种产品的单价波动小；

(3) 该厂决定第四次该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件上调m%（m＞0），使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1，求m的值．

【考点】

统计表; 折线统计图; 平均数及其计算; 方差;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

根据上表数据绘制的折线统计图如图所示：

综合题普通

甲公司为“基本工资 $\text{[math]}$ 揽件提成”，其中基本工资为70元/日，每揽收一件提成2元；

乙公司无基本工资，仅以揽件提成计算工资．若当日揽件数量不超过 $\text{[math]}$ 件，则每件提成 $\text{[math]}$ 元；若当日搅件数超过 $\text{[math]}$ 件，则超过部分每件提成 $\text{[math]}$ 元．

如图是今年四月份甲公司揽件员人均揽件数和乙公司揽件员人均揽件数的条形统计图：

根据以上信息．以今年四月份的数据为依据．并将各公司揽件员的人均揽件数视为该公司各揽件员的揽件数．解决以下问题：

综合题普通

具体操作分为四步：

第一步：计算小明这三次模拟考试中语文、数学、英语单科成绩与当次考试该科年级最高分的差值作为“相对失分”，并记录如下：

小明这三次模拟考试中语文、数学、英语每科成绩“相对失分”表．

第二步：计算表中每科成绩的“相对失分”的平均数，并分别记作： $\text{[math]}$ 语文， $\text{[math]}$ 数学， $\text{[math]}$ 英语；

第三步：计算表中每科成绩的“相对失分比”；

某一科成绩的“相对失分比”= $\text{[math]}$ ×100%

例：语文成绩的“相对失分比”= $\text{[math]}$ ×100%．

第四步：根据“相对失分比”划分复习时间，即某科的“相对失分比”就是该科周末复习时间的占比．

根据以上操作步骤，解答下列问题：

综合题普通