1.
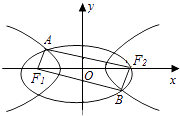
在直角坐标系  中,椭圆
中,椭圆  的中心在原点,焦点在
的中心在原点,焦点在  轴上,且过点
轴上,且过点  ,若
,若  的两焦点与其中一个顶点能构成一个等边三角形.
的两焦点与其中一个顶点能构成一个等边三角形.

(1)
求  的方程.
(2)
已知过
的方程.
(2)
已知过  的两条直线
的两条直线  ,
,  (斜率都存在)与
(斜率都存在)与  的右半部分(
的右半部分(  轴右侧)分别相交于
轴右侧)分别相交于  ,
,  两点,且
两点,且  的面积为
的面积为  ,试判断
,试判断  ,
,  的斜率之积是否为定值?若是,求出定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出定值;若不是,说明理由.
【考点】
椭圆的简单性质;