如图，PA是⊙O的切线，切点为A，AC是⊙O的直径，连接OP交⊙O于E.过A点作AB⊥PO于点D，交⊙O于B，连接BC，P B.

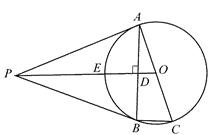
1. 如图，PA是⊙O的切线，切点为A，AC是⊙O的直径，连接OP交⊙O于E.过A点作AB⊥PO于点D，交⊙O于B，连接BC，P B.

(1) 求证：PB是⊙O的切线；

(2) 求证：E为△PAB的内心；

(3) 若cos∠PAB= $\text{[math]}$ ，BC=1，求PO的长.

【考点】

三角形全等及其性质; 三角形全等的判定; 圆心角、弧、弦的关系; 切线的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图， $\text{[math]}$ 为等边 $\text{[math]}$ 的外接圆，半径为2，点 $\text{[math]}$ 在劣弧 $\text{[math]}$ 上运动（不与点 $\text{[math]}$ 重合），连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ 是 $\text{[math]}$ 的平分线；

(2) 四边形 $\text{[math]}$ 的面积 $\text{[math]}$ 是线段 $\text{[math]}$ 的长 $\text{[math]}$ 的函数吗？如果是，求出函数解析式；如果不是，请说明理由；

(3) 若点 $\text{[math]}$ 分别在线段 $\text{[math]}$ ， $\text{[math]}$ 上运动（不含端点），经过探究发现，点 $\text{[math]}$ 运动到每一个确定的位置， $\text{[math]}$ 的周长有最小值 $\text{[math]}$ ，随着点 $\text{[math]}$ 的运动， $\text{[math]}$ 的值会发生变化，求所有 $\text{[math]}$ 值中的最大值．

综合题普通

2. ∆ABC中，点D在直线AB上.点E在平面内，点F在BC的延长线上，∠E=∠BDC，AE=CD，∠EAB+∠DCF=180º．

(1) 如图①，求证AD+BC=BE；

(2) 如图②、图③，请分别写出线段AD，BC，BE之间的数量关系，不需要证明；

(3) 若BE⊥BC，tan∠BCD= $\text{[math]}$ ，CD=10，则AD=．

综合题困难

3. 已知：如图，在五边形ABCDE中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .

(1) 求证： $\text{[math]}$ .

(2) 当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的度数.

综合题普通