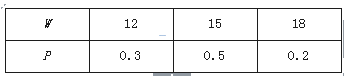
1.
设甲、乙两位同学上学期间,每天7:30之前到校的概率均为  .假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量
的分布列和数学期望;
(Ⅱ)设 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件
发生的概率.
【考点】
离散型随机变量及其分布列;
离散型随机变量的期望与方差;
二项分布;
能力提升
变式训练
拓展培优
真题演练