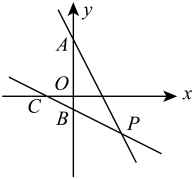
如图，在平面直角坐标系xOy中，直线AP交x轴于点P（p，0），交y轴于点A（0，a），且a、p满足 +（p+1）2=0．

1. 如图，在平面直角坐标系xOy中，直线AP交x轴于点P（p，0），交y轴于点A（0，a），且a、p满足 $\text{[math]}$ +（p+1）²=0．

(1) 求直线AP的解析式；

(2) 如图1，点P关于y轴的对称点为Q，R（0，2），点S在直线AQ上，且SR=SA，求直线RS的解析式和点S的坐标；

(3) 如图2，点B（-2，b）为直线AP上一点，以AB为斜边作等腰直角三角形ABC，点C在第一象限，D为线段OP上一动点，连接DC，以DC为直角边，点D为直角顶点作等腰三角形DCE，EF⊥x轴，F为垂足，下列结论：①2DP+EF的值不变；② $\text{[math]}$ 的值不变；其中只有一个结论正确，请你选择出正确的结论，并求出其定值．

【考点】

一次函数图象与几何变换;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ．

(1) 求出m ， n的值；

(2) 观察图象，写出 $\text{[math]}$ 的解集；

(3) 设 $\text{[math]}$ 和 $\text{[math]}$ 的面积分别为 $\text{[math]}$ 、 $\text{[math]}$ ，求 $\text{[math]}$ ．

综合题普通

2. 如图1，在平面直角坐标系xOy中，点O是坐标原点，直线 $\text{[math]}$ ： $\text{[math]}$ 与直线 $\text{[math]}$ ： $\text{[math]}$ 交于点A，两直线与x轴分别交于点 $\text{[math]}$ 和 $\text{[math]}$ .

(1) 求直线 $\text{[math]}$ 和 $\text{[math]}$ 的表达式.

(2) 点P是y轴上一点，当 $\text{[math]}$ 最小时，求点P的坐标.

(3) 如图2，点D为线段 $\text{[math]}$ 上一动点，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折得到 $\text{[math]}$ ，线段 $\text{[math]}$ 交x轴于点F，若 $\text{[math]}$ 为直角三角形，求点D坐标.

综合题困难

3. 如图，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴分别交于 $\text{[math]}$ .点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .

(1) 求直线的解析式；

(2) 若点 $\text{[math]}$ 是第二象限内的直线上的一个动点，当点 $\text{[math]}$ 运动过程中，试写出三角形 $\text{[math]}$ 的面积S与 $\text{[math]}$ 的函数关系式，并写出自变量 $\text{[math]}$ 的取值范围；

(3) 探究：当 $\text{[math]}$ 运动到什么位置时，三角形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，并说明理由.

综合题普通