如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD

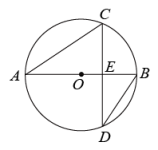
1. 如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD

(1) 求证：BD平分∠ABC；

(2) 当∠ODB=30°时，求证：BC=OD．

【考点】

垂径定理; 圆周角定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在锐角△ABC中，AB＞AC，AD⊥BC于点D，以AD为直径的⊙O分别交AB，AC于点E，F，连接DE，DF.

(1) 求证：∠EAF＋∠EDF＝180°.

(2) 已知P是射线DC上一个动点，当点P运动到PD＝BD时，连接AP，交⊙O于点G，连接DG.设∠EDG＝∠α，∠APB＝∠β，那么∠α与∠β有何数量关系？试证明你的结论(在探究∠α与∠β的数量关系时，必要时可直接运用(1)的结论进行推理与解答)．

综合题困难

2. 如图，AB是⊙O的直径，BC是⊙O的弦，OD⊥CB于点E，交BC于点E．

(1) 请写出三个不同类型的正确结论；

(2) 连接CD，∠ABC=20°，求∠CDE的度数．

综合题普通

3. 如图，⊙O的半径OD⊥弦AB于点C，联结AO并延长交⊙O于点E，联结EC．已知AB=8，CD=2．

(1) 求OA的长度；

(2) 求CE的长度．

综合题普通