已知∠α的顶点在正n边形的中心点O处，∠α绕着顶点O旋转，角的两边与正n边形的两边分别交于点M、N，∠α与正n边形重叠部分面积为S．

1. 已知∠α的顶点在正n边形的中心点O处，∠α绕着顶点O旋转，角的两边与正n边形的两边分别交于点M、N，∠α与正n边形重叠部分面积为S．

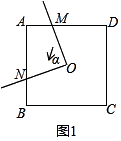
(1) 当n=4，边长为2，∠α=90°时，如图（1），请直接写出S的值；

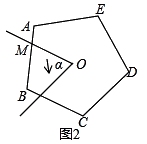
(2) 当n=5，∠α=72°时，如图（2），请问在旋转过程中，S是否发生变化？并说明理由；

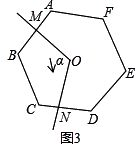
(3) 当n=6，∠α=120°时，如图（3），请猜想S是原正六边形面积的几分之几（不必说明理由）．若∠α的平分线与BC边交于点P，判断四边形OMPN的形状，并说明理由．

【考点】

全等三角形的判定与性质; 正方形的性质; 圆内接正多边形; 几何图形的面积计算-割补法;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在 $\text{[math]}$ 中， $\text{[math]}$ ，点D（与点 $\text{[math]}$ 不重合）为射线 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为一边且在 $\text{[math]}$ 的右侧作正方形 $\text{[math]}$ ．

(1) 如果 $\text{[math]}$ ．如图①，且点D在线段 $\text{[math]}$ 上运动．试判断线段 $\text{[math]}$ 与 $\text{[math]}$ 之间的位置关系，并证明你的结论．

(2) 如果 $\text{[math]}$ ，如图②，且点D在线段 $\text{[math]}$ 上运动．（1）中结论是否成立，为什么？

(3) 若正方形 $\text{[math]}$ 的边 $\text{[math]}$ 所在直线与线段 $\text{[math]}$ 所在直线相交于点P，设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．（用含x的式子表示）．

综合题普通

2. 如图，已知正方形ABCD的边长为1，正方形CEFG的面积为 $\text{[math]}$ ，点E在CD边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为 $\text{[math]}$ ，且 $\text{[math]}$ .

(1) 求线段CE的长；

(2) 若点H为BC边的中点，连结HD，求证： $\text{[math]}$ .

综合题普通

3. 如图，线段AB=8，射线BG⊥AB，P为射线BG上一点，以AP为边作正方形APCD，且点C、D与点B在AP两侧，在线段DP上取一点E，使∠EAP=∠BAP．直线CE与线段AB相交于点F(点F与点A、B不重合)

(1) 求证：△AEP≌△CEP；

(2) 判断CF与AB的位置关系，并说明理由；

(3) 求△AEF的周长。

综合题困难