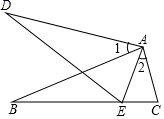
1.
如图,在 中,
中, ,
,  .点D是
.点D是 的中点,点E为边
的中点,点E为边 上一点,连接
上一点,连接 ,
,  , 以
, 以 为边在
为边在 的左侧作等边三角形
的左侧作等边三角形 , 连接
, 连接 .
.

(1)
求证: 为等边三角形;
(2)
求证:
为等边三角形;
(2)
求证: ;
;
【考点】
三角形全等及其性质;
等边三角形的判定与性质;
含30°角的直角三角形;
三角形全等的判定-SAS;
直角三角形斜边上的中线;