1.
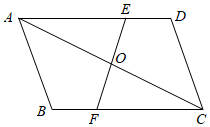
小静在学习平行四边形时发现:在平行四边形ABCD中,O为对角线BD的中点,过点O
的直线分别交AB , CD于点E , F , 连接DE , BF , 则四边形DEBF也是平行四边形.
她的证明思路是:利用平行四边形的性质得三角形全等,再利用平行四边形的判定定理,从而使问题得以解决.请根据小静的思路将下面证明过程补充完整.

证明:∵O为BD的中点,
∴ ① .
∵四边形ABCD是平行四边形,
∴ ② ,
∴∠BEO=∠DFO .
在△BOE和△DOF中,
∴△BOE≌△DOF(A.A.S.).
∴ ④ .
又∵OB=OD ,
∴四边形DEBF是平行四边形( ⑤ ).
【考点】
平行四边形的性质;
三角形全等的判定-AAS;
基础巩固
能力提升
变式训练
拓展培优
真题演练