1.
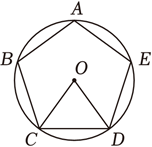
我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算.如图, 的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计
的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计 的面积,可得π的估计值为
的面积,可得π的估计值为 , 若用圆内接正十二边形作近似估计,可得π的估计值为( )
, 若用圆内接正十二边形作近似估计,可得π的估计值为( )

A.
 B.
B.
 C.
3
D.
C.
3
D.

【考点】
三角形的面积;
圆内接正多边形;
正多边形的性质;
基础巩固
能力提升
变式训练