1.
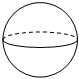
如图所示的平面图形绕直线 旋转一周,可以得到的立体图形是( )
旋转一周,可以得到的立体图形是( )
![]()
A.
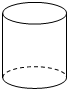
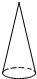 B.
B.
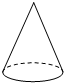
 C.
C.
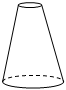
 D.
D.

【考点】
点、线、面、体及之间的联系;