1.
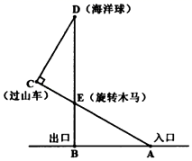
如图,在△ABC中,∠B=45°, , 等腰直角△DAE中,∠DAE=90°,且点D是边BC上一点.
, 等腰直角△DAE中,∠DAE=90°,且点D是边BC上一点.

(1)
求 的长;
(2)
如图1,当点
的长;
(2)
如图1,当点 恰在
恰在 上时,求点
上时,求点 到
到 的距离;
(3)
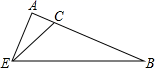
如图2,当点
的距离;
(3)
如图2,当点 从点
从点 向点
向点 运动时,求点
运动时,求点 到
到 的距离的最大值.
的距离的最大值.
【考点】
含30°角的直角三角形;
勾股定理;
等腰直角三角形;
三角形全等的判定-AAS;