1.
在“双减”背景下,某区教育部门想了解该区A,B两所学校九年级各500名学生的课后书面作业时长情况,从这两所学校分别随机抽取50名九年级学生的课后书面作业时长数据(保留整数),整理分析过程如下:
【收集数据】A学校50名九年级学生中,课后书面作业时长在70.5≤x<80.5组的具体数据如下:
74,72,72,73,74,75,75,75,75,
75,75,76,76,76,77,77,78,80
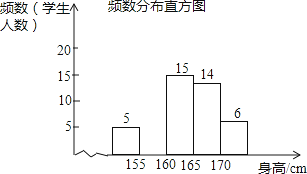
【整理数据】不完整的两所学校的频数分布表如下,不完整的A学校频数分布直方图如图所示:
|
组别 |
50.5≤x<60.5 |
60.5≤x<70.5 |
70.5≤x<80.5 |
80.5≤x<90.5 |
90.5≤x<100.5 |
|
A学校 |
5 |
15 |
x |
8 |
4 |
|
B学校 |
7 |
10 |
12 |
17 |
4 |

【分析数据】两组数据的平均数、众数、中位数、方差如下表:
|
特征数 |
平均数 |
众数 |
中位数 |
方差 |
|
A学校 |
74 |
75 |
y |
127.36 |
|
B学校 |
74 |
85 |
73 |
144.12 |
根据以上信息,回答下列问题:
(1)
本次调查是调查(选填“抽样”或“全面”);
(2)
统计表中,x=,y=;
(3)
补全频数分布直方图;
(4)
在这次调查中,课后书面作业时长波动较小的是学校(选填“A”或“B”);
(5)
按规定,九年级学生每天课后书面作业时长不得超过90分钟,估计两所学校1000名学生中,能在90分钟内(包括90分钟)完成当日课后书面作业的学生共有人.
【考点】
用样本估计总体;
频数(率)分布表;
频数(率)分布直方图;
中位数;
方差;
能力提升