1.
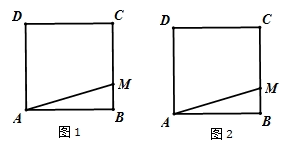
已知:边长为4的正方形ABCD,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=45°,连接EF.求证:EF=BE+DF.
思路分析:
(1)
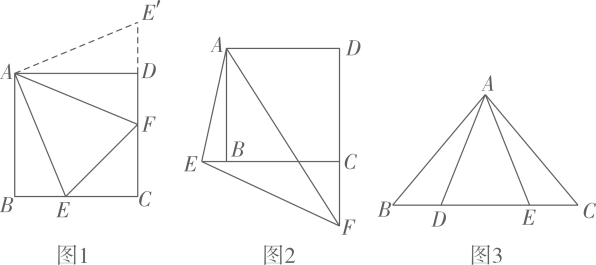
如图1,∵正方形ABCD中,AB=AD,∠BAD=∠B=∠ADC=90°,
(2)
类比探究:
如图2,当点E在线段CB的延长线上,探究EF、BE、DF之间存在的数量关系,并写出证明过程;
(3)
拓展应用:
如图3,在△ABC中,AB=AC,D、E在BC上,∠BAC=2∠DAE.若S△ABC=14,S△ADE=6,求线段BD、DE、EC围成的三角形的面积.
∴把△ABE绕点A逆时针旋转90°至△ADE',则F、D、E'在一条直线上,
∠E'AF=度,……
根据定理,可证:△AEF≌△AE'F.
∴EF=BE+DF.
如图2,当点E在线段CB的延长线上,探究EF、BE、DF之间存在的数量关系,并写出证明过程;
如图3,在△ABC中,AB=AC,D、E在BC上,∠BAC=2∠DAE.若S△ABC=14,S△ADE=6,求线段BD、DE、EC围成的三角形的面积.
【考点】
正方形的性质;
旋转的性质;
几何图形的面积计算-割补法;
三角形全等的判定-SAS;