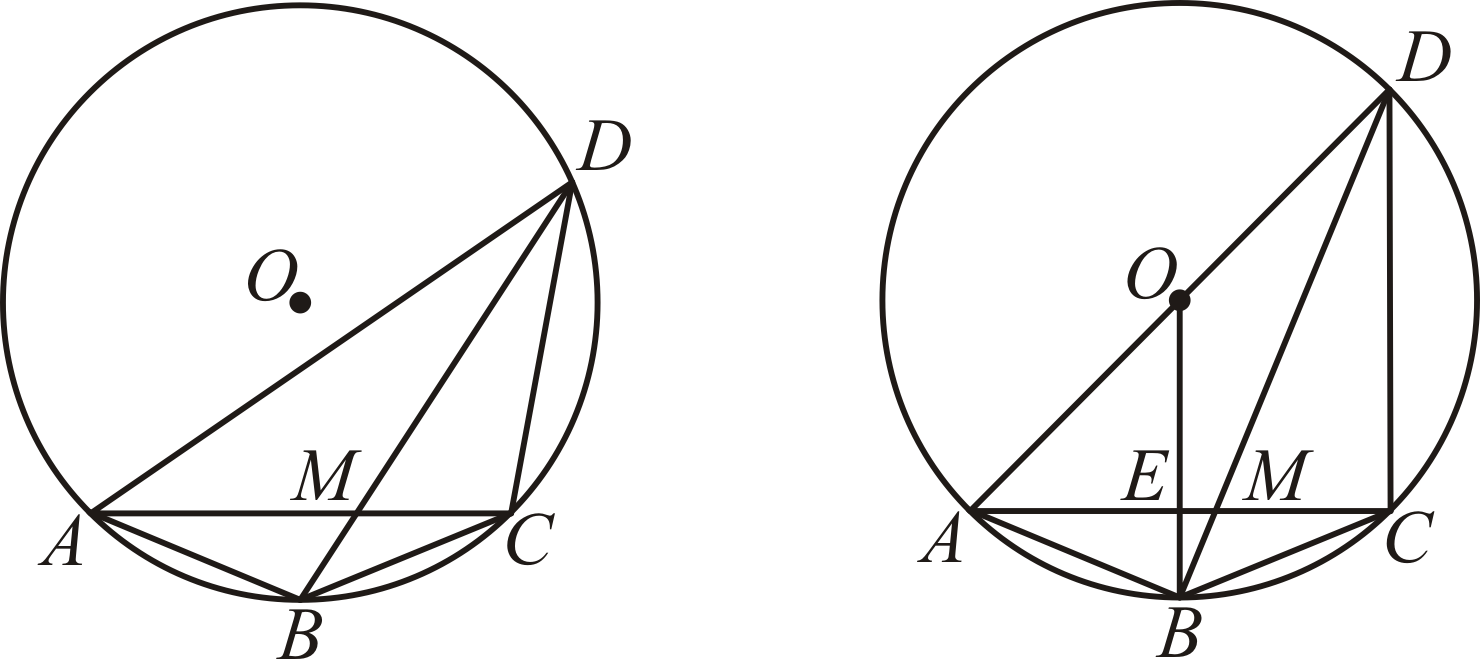如图1，⊙O为锐角三角形ABC的外接圆，点D在BC上，AD交BC于点E，点F在AE上，满足∠AFB-∠BFD=∠ACB，FG∥AC交BC于点G，BE=FG，连结BD，DG．设∠ACB=α．

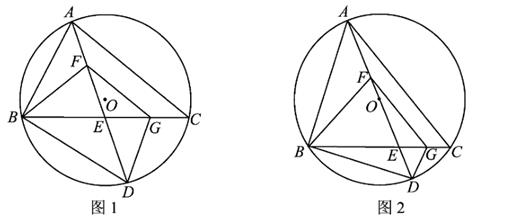
1. 如图1，⊙O为锐角三角形ABC的外接圆，点D在BC上，AD交BC于点E，点F在AE上，满足∠AFB-∠BFD=∠ACB，FG∥AC交BC于点G，BE=FG，连结BD，DG．设∠ACB=α．

(1) 用含α的代数式表示∠BFD．

(2) 求证：△BDE≌△FDG．

(3) 如图2，AD为⊙O的直径．

①当 $\text{[math]}$ 的长为2时，求 $\text{[math]}$ 的长．

②当OF：OE=4：11时，求cosα的值．

【考点】

圆的综合题; 相似三角形的判定与性质; 锐角三角函数的定义; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在 $\text{[math]}$ 中，直径 $\text{[math]}$ 垂直弦 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，作 $\text{[math]}$ 于点 $\text{[math]}$ ，交线段 $\text{[math]}$ 于点 $\text{[math]}$ （不与点 $\text{[math]}$ 重合），连接 $\text{[math]}$ ．

(1) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

(2) 求证： $\text{[math]}$ ．

(3) 若 $\text{[math]}$ ，猜想 $\text{[math]}$ 的度数，并证明你的结论．

综合题困难

2. 如图， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的两条直径， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ， $\text{[math]}$ ，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

(2) 求证： $\text{[math]}$ ．

(3) 设 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ，求证： $\text{[math]}$ ．

综合题困难

3. 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，对角线 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ．

(2) 当 $\text{[math]}$ 时，记 $\text{[math]}$ ，记 $\text{[math]}$ ．

①当 $\text{[math]}$ 时，求t的值；

②求t的最大值．

(3) 当 $\text{[math]}$ 为直径时，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点E，满足以下条件：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ （m，n均为正整数）；求 $\text{[math]}$ 的半径r的值．

综合题困难