1.
如图,AB是⊙O的直径,弦CD⊥OA于点E,连结OC,OD.若⊙O的半径为m,∠AOD=∠α,则下列结论一定成立的是( )
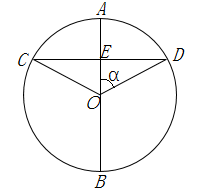
A.
oE=m•tanα
B.
CD=2m•sinα
C.
AE=m•cosα
D.
S△COD=m2•sinα
【考点】
三角形的面积;
垂径定理;
解直角三角形;







