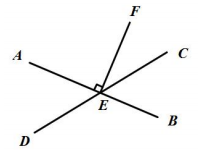
1.
如图  ,垂足为D ,
,垂足为D ,  ,下列结论正确的有( )
,下列结论正确的有( )
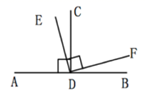
⑴ ;(2)
;(3)
与
互余;(4)
与
互补.
A.
1个
B.
2个
C.
3个
D.
4个
【考点】
余角、补角及其性质;