1.
如图,将边长为  的正三角形纸片
的正三角形纸片  按如下顺序进行两次折叠,展开后,得折痕
按如下顺序进行两次折叠,展开后,得折痕  ,
,  (如图①),点
(如图①),点  为其交点.
为其交点.

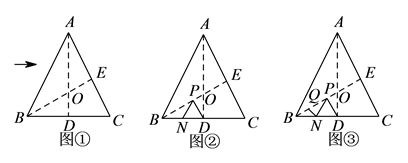
(1)
探求  到与
到与 的数量关系,并说明理由.
(2)
如图②,若
的数量关系,并说明理由.
(2)
如图②,若  ,
,  分别为
分别为  ,
,  上的动点.
上的动点.
① 当 的长度取得最小值时,求
的长度.
【考点】
等腰三角形的性质;
等边三角形的判定与性质;
含30°角的直角三角形;
轴对称的应用-最短距离问题;


