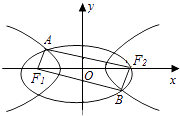
设椭圆：的离心率与双曲线的离心率互为倒数，且椭圆的长轴长为4．

1. 设椭圆 $\text{[math]}$ ： $\text{[math]}$ 的离心率与双曲线 $\text{[math]}$ 的离心率互为倒数，且椭圆的长轴长为4．

(1) 求椭圆 $\text{[math]}$ 的标准方程；

(2) 若直线 $\text{[math]}$ 交椭圆 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 两点， $\text{[math]}$ （ $\text{[math]}$ ）为椭圆 $\text{[math]}$ 上一点，求 $\text{[math]}$ 面积的最大值．

【考点】

椭圆的简单性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 给定椭圆 $\text{[math]}$ ，称圆 $\text{[math]}$ 为椭圆 $\text{[math]}$ 的“伴随圆”.已知点 $\text{[math]}$ 是椭圆 $\text{[math]}$ 上的点

(1) 若过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与椭圆 $\text{[math]}$ 有且只有一个公共点，求 $\text{[math]}$ 被椭圆 $\text{[math]}$ 的伴随圆 $\text{[math]}$ 所截得的弦长：

(2) $\text{[math]}$ 是椭圆 $\text{[math]}$ 上的两点，设 $\text{[math]}$ 是直线 $\text{[math]}$ 的斜率，且满足 $\text{[math]}$ ，试问：直线 $\text{[math]}$ 是否过定点，如果过定点，求出定点坐标，如果不过定点，试说明理由。

解答题普通

2. 已知椭圆C的两个焦点是F₁（﹣2，0），F₂（2，0），且椭圆C经过点A（0， $\text{[math]}$ ）．

(1) 求椭圆C的标准方程；

(2) 若过椭圆C的左焦点F₁（﹣2，0）且斜率为1的直线l与椭圆C交于P、Q两点，求线段PQ的长（提示：|PQ|= $\text{[math]}$ |x₁﹣x₂|）．

解答题普通

3. 已知椭圆E： $\text{[math]}$ =1的离心率为 $\text{[math]}$ ，点F₁ ， F₂是椭圆E的左、右焦点，过F₁的直线与椭圆E交于A，B两点，且△F₂AB的周长为8．

(1) 求椭圆E的标准方程；

(2) 动点M在椭圆E上，动点N在直线l：y=2 $\text{[math]}$ 上，若OM⊥ON，探究原点O到直线MN的距离是否为定值，并说明理由．

解答题普通