如图，在Rt△ABC中，∠C=90°，点D在线段AB上，以AD为直径的⊙O与BC相交于点E，与AC相交于点F，∠B=∠BAE=30°．

1. 如图，在Rt△ABC中，∠C=90°，点D在线段AB上，以AD为直径的⊙O与BC相交于点E，与AC相交于点F，∠B=∠BAE=30°．

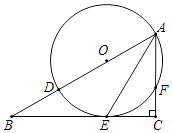
(1) 求证：BC是⊙O的切线；

(2) 若AC=3，求⊙O的半径r；

(3) 在（1）的条件下，判断以A、O、E、F为顶点的四边形为哪种特殊四边形，并说明理由．

【考点】

菱形的判定; 圆周角定理; 切线的判定; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图， $\text{[math]}$ 的半径为2，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ．

(1) 求证：四边形 $\text{[math]}$ 为菱形．

(2) 判断 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由．

综合题普通

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，垂足为 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线．

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通

3. 如图，已知AB为⊙O的直径，F为⊙O上一点，AC平分∠BAF且交⊙O于点C，过点C作CD⊥AF于点D，延长AB、DC交于点E，连接BC，CF．

(1) 求证：CD是⊙O的切线；

(2) 若AD=6，DE=8，求BE的长；

(3) 求证：AF+2DF=AB．

综合题普通