0 返回首页
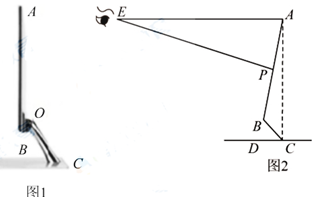
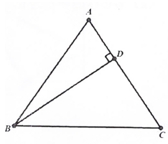
1. 已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O顺时针旋转60°，如题图1，连接BC．

(1) 填空：∠OBC=°；
(2) 如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；
(3) 如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？
【考点】
三角形的面积; 锐角三角函数的定义; 旋转的性质; 三角形-动点问题;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 如图，网格中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．

(1) 在图中确定点C，点C在小正方形的顶点上，请你连接CA，CB，BC＝4 ；
(2) 在（1）确定点C后，在网格内确定点D，点D在小正方形的顶点上，请你连接CD，BD，CD∥AB，△CDB的面积为6，直接写出∠CBD的正切值．
综合题 普通
2. 在“停课不停学”期间，小明用电脑在线上课，图1是他的电脑液晶显示器的侧面图，显示屏AB可以绕点O旋转一定的角度．研究表明：当眼睛E与显示屏顶端A在同一水平线上，且望向显示器屏幕形成一个18°的俯角（即望向屏幕中心P的视线EP与水平线EA的夹角∠AEP）时，对保护眼睛比较好，而且显示屏顶端A与底座C的连线AC与水平线CD垂直时（如图2）时，观看屏幕最舒适。此时测得∠BCD=30°，∠APE=90°，液晶显示屏的宽AB为32cm。

(1) 求眼睛E与显示屏顶端A的水平距离AE．（结果精确到1cm）
(2) 求显示屏顶端A与底座C的距离AC。（结果精确到1cm）

（参考数据：sin18°≈0.3，cos18°≈0.9，tan18°≈0.3， ≈1.4， ≈1.7）
综合题 普通
3. 如图，△ABC中，AB=AC=13，BD⊥AC于点D，sinA= ．

(1) 求BD的长.
(2) 求tanC的值．
综合题 普通