某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为批物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合，如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系。

1. 某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为批物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合，如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系。

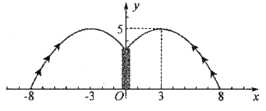
(1) 求水柱所在抛物线（第一象限部分）的函数表达式；

(2) 王师傅在水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

(3) 经检修评估，游乐园决定对喷水设施做如下设计改进；在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后水热水柱的最大高度。

【考点】

二次函数的实际应用-喷水问题; 二次函数与一元二次方程的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 为了给观光绿化带浇水，拟安装一排喷水口，如图 $\text{[math]}$ 为喷水口喷水的横截面，该喷水口 $\text{[math]}$ 离地竖直高度 $\text{[math]}$ 为 $\text{[math]}$ ，可以把喷出水的上、下边缘抽象为两条抛物线的部分图象：把绿化带横截面抽象为矩形 $\text{[math]}$ ，其中 $\text{[math]}$ ，其下边缘抛物线是由上边缘抛物线向左平移得到，上边抛物线最高点 $\text{[math]}$ 离喷水口的水平距离为 $\text{[math]}$ ，高出喷水口 $\text{[math]}$ ，喷水口到绿化带的水平距离 $\text{[math]}$ 为 $\text{[math]}$ （单位： $\text{[math]}$ ）．

(1) 求上边缘抛物线的函数解析式，并求喷出水的最大射程 $\text{[math]}$ ；

(2) 通过计算求点 $\text{[math]}$ 的坐标；

(3) 绿化带右侧（图中点 $\text{[math]}$ 的右侧） $\text{[math]}$ 米外是人行道，要使喷出的水能浇灌到整个绿化带，同时不会淋湿行人，直接写出 $\text{[math]}$ 的取值范围．

综合题普通

2. 如图①，利用喷水头喷出的水对小区草坪进行喷灌作业是养护草坪的一种方法.如图②，点 $\text{[math]}$ 处有一个喷水头，距离喷水头 $\text{[math]}$ 的 $\text{[math]}$ 处有一棵高度是 $\text{[math]}$ 的树，距离这棵树 $\text{[math]}$ 的 $\text{[math]}$ 处有一面高 $\text{[math]}$ 的围墙，建立如图所示的平面直角坐标系，已知某次浇灌时，喷水头喷出的水柱的坚直高度 $\text{[math]}$ (单位： $\text{[math]}$ )与水平距离 $\text{[math]}$ (单位： $\text{[math]}$ 近似满足函数关系 $\text{[math]}$ .

(1) 某次喷水浇灌时，测得 $\text{[math]}$ 与 $\text{[math]}$ 的几组数据如下：

$\text{[math]}$	0	2	6	10	12	14	16
$\text{[math]}$	0	0.88	2.16	2.80	2.88	2.80	2.56

①根据上述数据，求这些数据满足的函数关系；

②判断喷水头喷出的水柱能否越过这棵树，并请说明理由；

(2) 某次喷水浇灌时，已知喷水头喷出的水柱的坚直高度 $\text{[math]}$ 与水平距离 $\text{[math]}$ 近似满足函数关系 $\text{[math]}$ .假设喷水头喷出的水柱能够越过这棵树，且不会浇到墙外，下面有四个关于 $\text{[math]}$ 的不等式：
A. $\text{[math]}$
B. $\text{[math]}$
C. $\text{[math]}$
D. $\text{[math]}$
其中正确的不等式是.(填上所有正确的选项)

综合题困难

3. 在平面直角坐标系 $\text{[math]}$ 中，已知抛物线 $\text{[math]}$ ．

(1) 求该抛物线的对称轴（用含a的式子表示）；

(2) 若 $\text{[math]}$ ，当 $\text{[math]}$ 时，求y的取值范围；

(3) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为该抛物线上的点，若 $\text{[math]}$ ，求a的取值范围．

综合题普通