如图1，在锐角△ABC中，∠ABC=45°，高线AD、BE相交于点F．

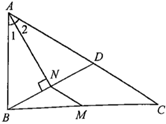
1. 如图1，在锐角△ABC中，∠ABC=45°，高线AD、BE相交于点F．

(1) 判断BF与AC的数量关系并说明理由；

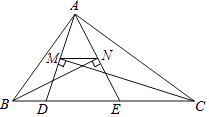
(2) 如图2，将△ACD沿线段AD对折，点C落在BD上的点M，AM与BE相交于点N，当DE∥AM时，判断NE与AC的数量关系并说明理由．

【考点】

全等三角形的判定与性质; 等腰三角形的判定与性质; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3

(1) 求证：BN=DN；

(2) 求△ABC的周长

综合题普通

2. 在平面直角坐标系 $\text{[math]}$ 中，已知点 $\text{[math]}$ ， $\text{[math]}$ ．对于点 $\text{[math]}$ 给出如下定义：将点 $\text{[math]}$ 先向右 $\text{[math]}$ 或向左 $\text{[math]}$ 平移 $\text{[math]}$ 个单位长度，再向上 $\text{[math]}$ 或向下 $\text{[math]}$ 平移 $\text{[math]}$ 个单位长度，得到点 $\text{[math]}$ ，点 $\text{[math]}$ 关于点 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，称点 $\text{[math]}$ 为点 $\text{[math]}$ 的“欢乐点”．

(1) 如图，点 $\text{[math]}$ $\text{[math]}$ ，点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上．若点 $\text{[math]}$ $\text{[math]}$ ，点 $\text{[math]}$ 为点 $\text{[math]}$ 的“欢乐点”．

①在图中画出点 $\text{[math]}$ 与点 $\text{[math]}$ ；

②连接 $\text{[math]}$ ，交线段 $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ ＝ $\text{[math]}$ $\text{[math]}$ ；

(2) ⊙O的半径为1， $\text{[math]}$ 是⊙O上一点，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，且 $\text{[math]}$ ＝ $\text{[math]}$ （ $\text{[math]}$ ＜ $\text{[math]}$ ＜1），若 $\text{[math]}$ 为⊙O外一点，点 $\text{[math]}$ 为点P的“欢乐点”，连接 $\text{[math]}$ ．当点 $\text{[math]}$ 在⊙O上运动时，直接写出 $\text{[math]}$ 长的最大值与最小值的差（用含 $\text{[math]}$ 的式子表示）．

综合题普通

3. 如图所示， $\text{[math]}$ 是 $\text{[math]}$ 的边 $\text{[math]}$ 的中点， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .

(1) 求证： $\text{[math]}$ .

(2) 求 $\text{[math]}$ 的周长.

综合题普通