1.
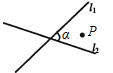
如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是( )
A.
1 号袋
B.
2 号袋
C.
3 号袋
D.
4 号袋
【考点】
作图﹣轴对称;