1.
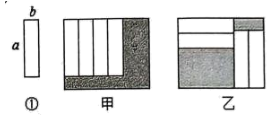
如图,甲、乙、丙三根笔直的钢管平行摆放在地面上。已知乙有一部分只与甲重叠,其余部分只与丙重叠,甲没有与乙重叠的部分的长度为2m ,丙没有与乙重叠的部分的长度为3m 。若乙的长度最长且甲、乙的长度相差 xm,乙、丙的长度相差 ym,则乙的长度为(用含有x,y的代数式表示)( )

A.
(x+y+5)m
B.
(x-y+5)m
C.
(2x+y-5)m
D.
(x+2y-5)m
【考点】
整式的加减运算;
用代数式表示几何图形的数量关系;