1.
有人设想:可以在飞船从运行轨道进入返回地球程序时,借飞船需要减速的机会,发射一个小型太空探测器,从而达到节能的目的.如图所示,飞船在圆轨道Ⅰ上绕地球飞行,其轨道半径为地球半径的k倍(k>1).当飞船通过轨道Ⅰ的A点时,飞船上的发射装置短暂工作,将探测器沿飞船原运动方向射出,并使探测器恰能完全脱离地球的引力范围,即到达距地球无限远时的速度恰好为零,而飞船在发射探测器后沿椭圆轨道Ⅱ向前运动,其近地点B到地心的距离近似为地球半径R.以上过程中飞船和探测器的质量均可视为不变.已知地球表面的重力加速度为g.

(1)求飞船在轨道Ⅰ运动的速度大小;
(2)若规定两质点相距无限远时引力势能为零,则质量分别为M.m的两个质点相距为r时的引力势能 , 式中G为引力常量.在飞船沿轨道Ⅰ和轨道Ⅱ的运动过程,其动能和引力势能之和保持不变;探测器被射出后的运动过程中,其动能和引力势能之和也保持不变.
①求探测器刚离开飞船时的速度大小;
②已知飞船沿轨道Ⅱ运动过程中,通过A点与B点的速度大小与这两点到地心的距离成反比.根据计算结果说明为实现上述飞船和探测器的运动过程,飞船与探测器的质量之比应满足什么条件.
【考点】
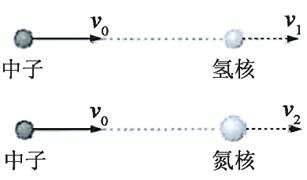
碰撞模型;
基础巩固
能力提升
变式训练
拓展培优
真题演练