1.
【项目式学习】在圆柱表面,蚂蚁怎么爬行路径最短? (π取3)
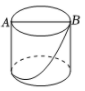
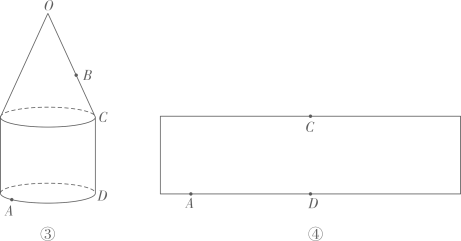
素材1:如图1,圆柱体的高AC为12cm,底面直径BC为6cm,在圆柱下底圆周上的A点有一只蚂蚁,它想吃到上底面圆周上与A 点对应的B 点处的食物.
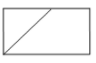
若蚂蚁沿图1中的折线A→C→B爬行的最短路径记为“路线一”,此时最短路程是 12+6=18cm. 将圆柱沿着AC将侧面展开得到图2,请在图2中画出蚂蚁爬行的最短路径记为“路线二”,此时最短路程是____ cm; 比较可知:蚂蚁爬行的最短路径是路线____(用“一”或“二”填空).


素材2:如图3所示的实践活动器材包括:底面直径为6cm,高为10cm的圆柱、橡皮筋、细线(借助细线来反映爬行的路线)、直尺,通过调节橡皮筋的位置达到改变圆柱的高度的目的.
(1)
两种路线路程的长度如表所示(单位:cm):
(2)
填空:表格中a的值是;表格中b表示的大小关系是;
(3)
经历上述探究后,请你思考:若圆柱的半径为r,圆柱的高为h. 在r不变的情况下,当圆柱半径为r与圆柱的高度h存在怎样的数量关系时,蚂蚁在圆柱表面的两种爬行路线的路程相等?
圆柱高度 | 沿路线一路程x | 沿路线二路程y | 比较x与y的大小 |
5 | 11 | x>y | |
4 | 10 | x>y | |
3 | a | 3 | b |
【考点】
勾股定理的实际应用-最短路径问题;