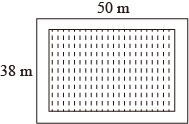
1.
如图,某小区规划在一个长为 、宽为
、宽为 的矩形场地
的矩形场地 上修建三条同样宽的小路,使其中两条与
上修建三条同样宽的小路,使其中两条与 平行,另一条与
平行,另一条与 平行,其余部分种草.若草坪部分的总面积为
平行,其余部分种草.若草坪部分的总面积为
 , 则小路的宽度为
, 则小路的宽度为 .
.

【考点】
一元二次方程的应用-几何问题;