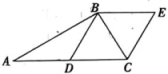
1.
在菱形 中,
中, , 点
, 点 是线段
是线段 上一动点,以
上一动点,以 为边向右侧作等边三角形
为边向右侧作等边三角形 , 点
, 点 的位置随着点
的位置随着点 的位置变化而变化.
的位置变化而变化.
(1)
如图 , 当点
, 当点 在菱形
在菱形 内部或边上时,连接
内部或边上时,连接 ,
(2)
若
,
(2)
若 , 点
, 点 为
为 的中点,则线段
的中点,则线段 的长最小值为_______最大值为________.
(3)
如图
的长最小值为_______最大值为________.
(3)
如图 , 当点
, 当点 在线段
在线段 的延长线上时,连接
的延长线上时,连接 , 若
, 若 ,
,  , 直接写出四边形
, 直接写出四边形 的面积________.
的面积________.
判断:与
的数量关系是__________请写出证明过程.
与
的位置关系是___________请写出证明过程.
【考点】
等边三角形的判定与性质;
勾股定理;
菱形的判定与性质;
三角形全等的判定-SAS;