1.
阅读与思考
下面是小文同学的数学日记，请仔细阅读并完成相应的任务．
构造同高三角形解决图形的面积问题 根据三角形中线的定义，可以证明中线将原三角形分成面积相等的两个三角形，我们还知道，只要两个三角形的高相同，那么他们的面积比等于底边之比，利用这两个结论可以在多边形中探索有关面积的问题，下面是我的思考过程：
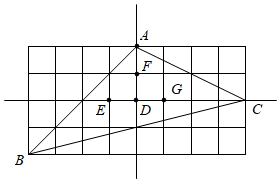
【发现结论】 如图1，在
【特例探究】 如图2，在任意四边形 证明思路如下： 连接 【一般探究】 如图3，在任意四边形 |
任务：
(1)
请将【特例探究】的过程补充完整；
(2)
【一般探究】中的结论为
与S的关系为：______．
(3)
如图4，若任意的十边形的面积为100，点K、L、M、N、O、P、Q、R分别是
、
、
、
、
、
、
、
边上离点A、C、E、E、F、H、I、A最近的四等分点，连接
、
、
、
、
、
、
、
， 则图中阴影部分的面积是______．
【考点】
三角形的角平分线、中线和高;
