如图1，某桥拱截面可视为抛物线的一部分，以O为坐标原点，所在直线为x轴建立平面直角坐标系．在某一时刻，桥拱内的水面宽米，桥拱顶点B到水面的距离是4米．

1. 如图1，某桥拱截面 $\text{[math]}$ 可视为抛物线的一部分，以O为坐标原点， $\text{[math]}$ 所在直线为x轴建立平面直角坐标系．在某一时刻，桥拱内的水面宽 $\text{[math]}$ 米，桥拱顶点B到水面的距离是4米．

(1) 求抛物线对应的函数解析式，并写出自变量x的取值范围；

(2) 要保证高2.26米的小船能够通过此桥（船顶与桥拱的距离不小于0.3米），求小船的最大宽度是多少？

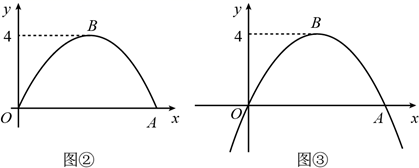
(3) 如图2，桥拱所在的抛物线在x轴下方部分与桥拱 $\text{[math]}$ 在平静水面中的倒影组成一个新函数图象，将新函数图象向右平移 $\text{[math]}$ 个单位长度，平移后的函数图象在 $\text{[math]}$ 时，y的值随x值的增大而减小，结合函数图象，直接写出n的取值范围．

【考点】

二次函数图象的几何变换; 二次函数的实际应用-拱桥问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，要修建一条截面为抛物线型的隧道，线段 $\text{[math]}$ 表示水平的路面，根据设计要求： $\text{[math]}$ ，该抛物线的顶点 $\text{[math]}$ 到 $\text{[math]}$ 的距离为 $\text{[math]}$ ．

(1) 请建立合适的平面直角坐标系，并求满足设计要求的抛物线的函数表达式；

(2) 现需在这一隧道内壁上同一高度处安装照明灯（即在该抛物线上的点 $\text{[math]}$ ， $\text{[math]}$ 处分别安装照明灯）．若要求 $\text{[math]}$ ， $\text{[math]}$ 处的照明灯水平距离为 $\text{[math]}$ ，求照明灯的高度．

综合题普通

2. 如图为抛物线形拱桥平面示意图，拱顶离水面 $\text{[math]}$ ，水面宽 $\text{[math]}$ ．以现有水平面的水平直线为 $\text{[math]}$ 轴，与抛物线形拱桥左边交点为原点建立平面直角坐标系．

(1) 求此抛物线解析式；

(2) 如图（1），若水面下降 $\text{[math]}$ ，水面宽度增加多少 $\text{[math]}$ ？

(3) 如图（2），为保证行船安全，在汛期来临之前，管理部门需要用一定长度的钢板搭建一个可调节大小的矩形“安全架”，露出水平面部分为 $\text{[math]}$ ，使点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线上，点 $\text{[math]}$ ， $\text{[math]}$ 为露出水面的端点，若确保点 $\text{[math]}$ ， $\text{[math]}$ 的间距不少于 $\text{[math]}$ ，求 $\text{[math]}$ 的最大长度．

综合题普通

3. 如图1，某公园在入园处搭建了一道“气球拱门”，拱门两端落在地面上．若将拱门看作抛物线的一部分，建立如图2所示的平面直角坐标系．当拱门上的点到 $\text{[math]}$ 点的水平距离为 $\text{[math]}$ （单位： $\text{[math]}$ ）时，它距地面的竖直高度为 $\text{[math]}$ （单位： $\text{[math]}$ ）．

(1) 经过对拱门进行测量，发现 $\text{[math]}$ 与 $\text{[math]}$ 的几组数据如下：

$\text{[math]}$	2	3	6	8	10	12
$\text{[math]}$	4	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	4	0

根据上述数据，直接写出该拱门的高度（即最高点到地面的距离）和跨度（即拱门底部两个端点间的距离），并求 $\text{[math]}$ 与 $\text{[math]}$ 满足的函数关系式．

(2) 在一段时间后，公园重新维修拱门．在同样的坐标系下，新拱门上的点距地面的竖直高度 $\text{[math]}$ （单位： $\text{[math]}$ ）与它到 $\text{[math]}$ 点的水平距离 $\text{[math]}$ （单位： $\text{[math]}$ ）近似满足函数关系 $\text{[math]}$ ，若记原拱门的跨度为 $\text{[math]}$ ，新拱门的跨度为 $\text{[math]}$ ，则 $\text{[math]}$ ______ $\text{[math]}$ （填“ $\text{[math]}$ ”，“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）．

综合题普通